Does Your Model Generalize or Memorize: Researchers find models with more parameters copy more bits from training sets

Benchmarks can measure how well large language models apply what they’ve learned from their training data to new data, but it’s harder to measure the degree to which they simply memorized their training data. New work proposes a way to gauge memorization.

What’s new: John X. Morris and colleagues at Meta, Google, Cornell University, and Nvidia developed a method that measures the number of bits a model memorizes during training.

Key insight: A model’s negative log likelihood is equal to the minimum number of bits needed to represent a given piece of data. The more likely the model is to generate the data, the fewer bits needed to represent it. If, to represent a given output, a hypothetical best model requires more bits than a trained model, then the trained model must have memorized that many bits of that output. The best model is hypothetical, but a better-performing model can stand in for it. The difference in the numbers of bits used to represent the output by this superior model and the trained model is a lower bound on the number of bits the trained model has memorized.

How it works: The authors trained hundreds of GPT-2 style models to predict the next token in two text datasets: (i) a synthetic dataset of 64-token strings in which each token was generated randomly and (ii) the FineWeb dataset of text from the web, its examples truncated to 64 tokens and deduplicated. They trained models from 100,000 to 20 million parameters on subsets of these datasets from 16,000 to 4 million examples. Then they computed the how much of the datasets the models had memorized:

• The authors computed the number of bits needed to represent each training example based on the likelihoods of the trained model and a superior model. For models trained on synthetic data, the superior model was the distribution used to generate the data. For models trained on a subset of FineWeb, they used GPT-2 trained on all FineWeb examples (after truncation and deduplication).
• They subtracted the number of bits computed for the superior model from the number computed for the trained model. A positive difference indicated the amount of memorization. A zero or negative difference indicated that memorization did not occur.
• To find the amount of data the model had memorized. they summed the number of bits memorized per example.

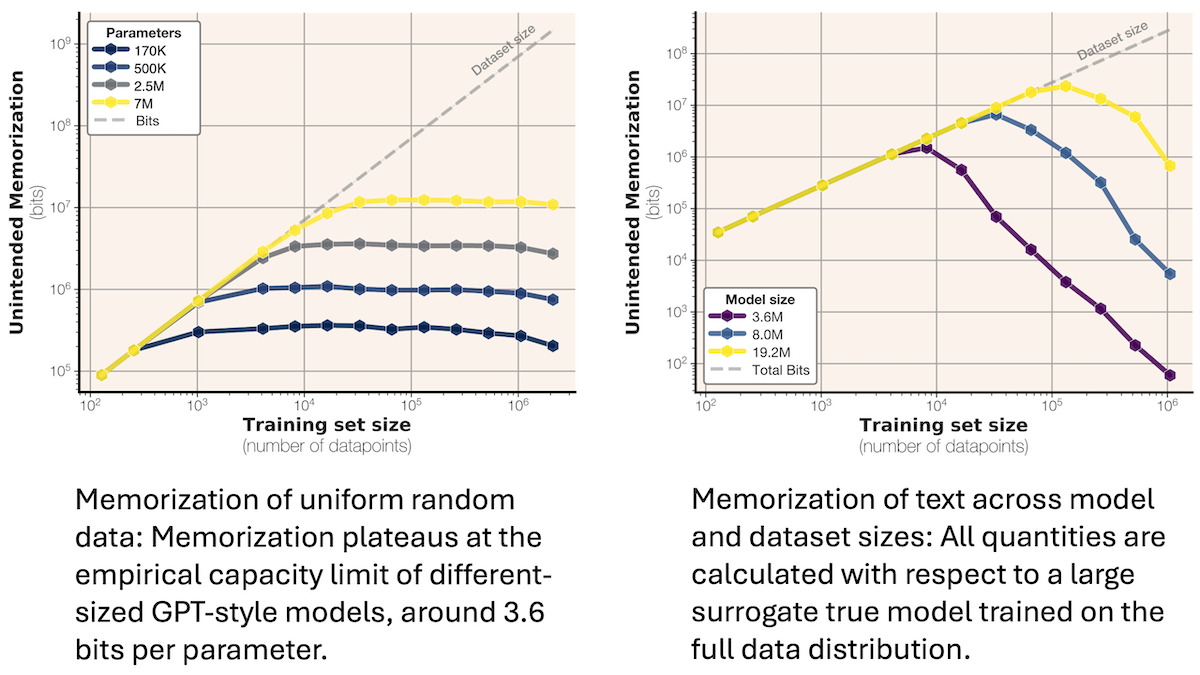
Results: The maximum number of bits a model memorized rose linearly with its parameter count regardless of the training dataset, amount of training data, or model size.

• Trained on synthetic data, a model’s memorization increased linearly and then plateaued after a certain amount of training data.
• Maximum memorization was approximately 3.5 to 3.6 bits per parameter (their models used 16 bits to represent each parameter).
• Trained on FineWeb, a model’s memorization increased linearly with the amount of training data before decreasing as the model started to generalize (that is, the number of bits memorized per parameter fell and benchmark scores rose). This result showed that models memorize until they reach a maximum capacity and then start to generalize.

Why it matters: Some previous efforts to measure memorization calculated the percentage of examples for which, given an initial sequence of tokens, a model would generate the rest. However, generating a repetitive sequence like “dog dog dog…” does not mean that a model has memorized it, and solving a simple arithmetic problem does not mean the model has memorized it or even encountered it in its training data. This work provides a theoretical basis for estimating how much of their training sets models memorize. It also lays a foundation for further work to reduce memorization without increasing the sizes of training datasets.

We’re thinking: It’s well known that more training data helps models to generalize. This work shows how to estimate the amount of data necessary before models begin to generalize.